Аналітична геометрія

Матеріал з Вікіпедії — вільної енциклопедії.
 
 

Аналіти́чна геоме́трія, розділ геометрії, у якому властивості геометричних об'єктів (точок, ліній, поверхонь) установлюються засобами алгебри за допомогою методу координат, тобто шляхом дослідження властивостей рівнянь, які і визначають ці об'єкти. Основні положення аналітичної геометрії вперше сформулював філософ і математик Рене Декарт в 1637 році. Лейбніц, Ісаак Ньютон і Леонард Ейлер надали аналітичній геометрії сучасної структури.

 

Історія

Створення аналітичної геометрії зазвичай приписують Рене Декарту, який виклав її основи в La Geometrie (Геометрія) , одного з трьох додатків, опублікованих в 1637 році разом зі своїм трактатом Міркування про метод. Спочатку робота не була добре прийнята, але після переведення латинськоюта додавання коментарів ван Схотена в 1649, трактат Декарта отримав належне визнання.

Основи

Характерною особливістю аналітичної геометрії є визначення геометричних фігур рівняннями. Нехай на площині з осями координат OX і OY (прямокутнадекартова система координат) маємо лінію l. Якщо вздовж l пересувати точку M, то координати x, y цієї точки будуть змінюватись, але між ними існуватиме певна залежність, яку можна записати у вигляді рівняння:

f(x, y) = 0 \,,

де f(x, y) є математичний вираз, що містить змінні x і y або одну з них.

Analityczna geometria example.png

Наприклад, з прямокутного трикутника OMP виводимо, що рівняння кола K радіуса г з центром в початку координат 0 є

x^2 + y^2 - r^2 = 0 .

Розглянемо ще пряму АВ. Якщо М є довільна її точка і OA = a, OB = b, то PA = a — x. З подібності прямокутних трикутників MPA і BOA маємо:

\frac{y}{a - x} = \frac{b}{ a} .

Звідси дістаємо рівняння прямої АВ:

bx + ay - ab = 0 \,.

В аналітичній геометрії приймають, що рівняння визначає геометричну фігуру як множину точок, координати х та у яких справджують це рівняння. Інакше кажучи, рівняння розглядають як засіб для поділу точок площини на 2 класи: до 1-го належать точки, координати яких справджують дане рівняння (ці точки утворюють визначену рівнянням фігуру), до 2-го — всі інші точки площини. Якщо рівняння алгебраїчне, то воно визначає лінію — дійсну чи уявну (див. нижче), яку називають алгебраїчною, а степінь рівняння — порядком цієї лінії. Порядок алгебраїчної лінії не залежить від того, як розміщені відносно неї осі координат. Прямі і тільки прямі є лініями 1-го порядку; конічні перерізи (тобто лінії, що утворюються при перетині конусу площиною) і тільки вони є лініями 2-го порядку. 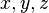Аналогічно рівняння f(x, y, z) = 0 , де x, y, z  — декартові координати точки у просторі, визначає просторову фігуру, зокрема алгебраїчну поверхню n-го порядку, якщо воно є алгебраїчним рівнянням n-го степеня. В сучасних курсах аналітичної геометрії вивчаються тільки лінії і поверхні 1-го та 2-го порядків.

Застосування в аналітичній геометрії алгебраїчних методів привело до поняття уявної фігури. Сукупність двох чисел x, y,  з яких принаймні одне уявне, можна розглядати як уявну точку. Якщо рівняння (наприклад , x^2 + y^2 + 1 = 0 ) справджують лише координати уявних точок, то вважають, що воно визначає уявну фігуру. Хоч поняттям нескінченно віддалених і уявних точок не відповідають жодні реальні образи, проте запровадження їх дозволило глибше досліджувати властивості фігур.

В сучасних курсах аналітичної геометрії широко використовується апарат векторного числення.

Див. також

Література

  • Українська радянська енциклопедія : у 12 томах / за ред. М. Бажана. — 2-ге вид. — К. : Головна редакція УРЕ, 1974–1985.
  • Білоусова В. П. та ін. Аналітична геометрія. К., 1957;
  • Привалов И. И. Аналитическая геометрия. Изд. 22. М., 1957;
  • Делоне Б. Н., Райков Д. А. Аналитическая геометрия, т. 1—2. М.—Л., 1948—49.

Посилання